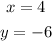Question

7x-y=342x+3y=-10. Solve each system of equations by graphing. Clearly identify your solution.

Answer 1

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

So, we must write each equation in Slope-Intercept form. We can do that solving for "y".

For Equation 1:

`\begin{gathered} 7x-y=34 \\ 7x-34=y \\ y=7x-34 \end{gathered}`

We can see that:

`\begin{gathered} m=7 \\ y=-34 \end{gathered}`

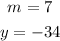
Knowing those values, we can graph the line.

For Equation 2:

`\begin{gathered} 2x+3y=-10 \\ 3y=-2x-10 \\ y=-(2)/(3)x-(10)/(3) \end{gathered}`

For this line:

`\begin{gathered} m=-(2)/(3) \\ b=-(10)/(3) \end{gathered}`

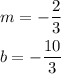
Knowing those values, we can graph the second line.

See the graph attached.

Observe that they intersect each other at the point (4,-6). That point of intersection is the solution of the System of equations:

`\begin{gathered} x=4 \\ y=-6 \end{gathered}`