Question

What are the solutions of the following system?

x^2+y^2=25
2x+y=-5
A. (0, –5) and (–5, 5)
B.(0, –5) and (5, –15)
C.(0, –5) and (–4, 3)
D.(0, –5) and (4, –13)

Answer 1

so what you do is solve for y in 2nd equation
minus 2x boh sides

y=-2x-5
sub that for y in other equation

x^2+(-2x-5)^2=25
x^2+4x^2+20x+25=25
5x^2+20x+25=25
mminus 25 both sides
5x^2+20x=0
factor
(x)(5x+20)=0
set to zero
x=0
5x+20=0
5x=-20
x=-4

sub back

y=-2x-5
y=-2(0)-5
y=-5
a point is (0,-5)
y=-2x-5
y=-2(-4)-5
y=-8-5
y=-13
another is (-4,-13)


(0,-5) and (-4,13)

I think it is C, but you forgot to put that 1 infront of the 3

Answer 2

Option C is correct

the solution for the given system of equation is, (0, -5) and (-4, 3)

Explanation:

Using identity:

`(a+b)^2=a^2+b^2+2ab`

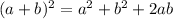
Given the equation:

`x^2+y^2=25` .....[1]

`2x+y=-5` .....[2]

We can write [2] as:

`y = -5-2x`

Substitute this in [1] we have;

`x^2+(-5-2x)^2=25`

Using identity rule;

`x^2+25+4x^2+20x = 25`

Combine like terms;

`5x^2+20x+25 = 25`

Subtract 25 from both sides we have;

`5x^2+20x=0`

⇒
`5x(x+4)=0`

By zero product property we have;

x = 0 and x+4 = 0

x = 0 and x = -4

Substitute these in [2] we have;

for x = 0

2(0)+y = -5

⇒
`y = -5`

For x = -4 ,

`2(-4)+y = -5`

-8+y = -5

add 8 to both sides we have;

y = 3

Therefore, the solution for the given system of equation is, (0, -5) and (-4, 3)