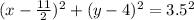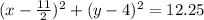Question

What is the equation of this circle in standard form?

Answer 1

i hope this helps you

Answer 2

Standard equation of circle:

`(x-(11)/(2))^2+(y-4)^2=12.25`

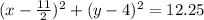
Explanation:

Given: Ends points of diameter are M(2,4) and N(9,4)

Mid point of M and N is center of circle.

Let center of circle be O(h,k)

Using mid point formula:

[tex[(x,y)\rightarrow (\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2})[/tex]

`O(h,k)\rightarrow ((2+9)/(2),(4+4)/(2))`

`O(h,k)\rightarrow ((11)/(2),4)`

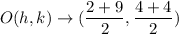
Distance between O and M is radius of circle.

Let radius of circle be r

Using distance formula:

`d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

`r=\sqrt{((11)/(2)-2)^2+(4-4)^2=3.5`

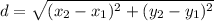
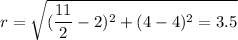
Standard equation of circle:

`(x-h)^2+(y-k)^2=r^2`

Equation of required circle:

`(x-(11)/(2))^2+(y-4)^2=3.5^2`

`(x-(11)/(2))^2+(y-4)^2=12.25`