Question

A 25-foot long ladder is propped against a wall at an angle of 18° with the wall. how high up the wall does the ladder reach? round the answer to the nearest tenth of a foot

Answer 1

here is the answer :)))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))

Answer 2

Find out the how high up the wall does the ladder reach .

To proof

let us assume that the height of the wall be x .

As given

A 25-foot long ladder is propped against a wall at an angle of 18° .

as shown in the diagram given below

By using the trignometric identity

`cos\theta = (Base)/(Hypotenuse)`

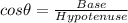
now

`\theta = 18^(\circ)`

Base = wall height = x

Hypotenuse = 25 foot

Put in the trignometric identity

`cos18^(\circ) = (x)/(25)`

`cos18^(\circ) = \bar{0.9510565162}`

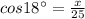
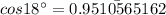
x = 23.8 foot ( approx)

Therefore the height of the ladder be 23.8 foot ( approx) .