Question

Calculate the wavelength of the electromagnetic radiation required to excite an electron from the ground state to the level with in a one-dimensional box 34.0 pm in length.

Answer 1

The question is incomplete. The complete question is :

Calculate the wavelength of the electromagnetic radiation required to excite an electron from the ground state to the level with n = 6 in a one-dimensional box 34.0 pm in length.

Solution :

In an one dimensional box, energy of a particle is given by :

`$E=(n^2h^2)/(8ma^2)$`

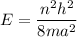
Here, h = Planck's constant

n = level of energy

= 6

m = mass of particle

a = box length

For n = 6, the energy associated is :

`$\Delta E = E_6 - E_1 $`

`$\Delta E = \left( (n_6^2h_2)/(8ma^2)\right) - \left( (n_1^2h_2)/(8ma^2)\right) $`

`$=(h^2(n_6^2 - n_1^2))/(8ma^2)$`

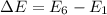
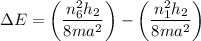
We know that,

`$E = (hc)/(\lambda) $`

Here, λ = wavelength

h = Plank's constant

c = velocity of light

So the wavelength,

`$= (hc)/(E)$`

`$=(hc)/((h^2(n_6^2 - n_1^2))/(8ma^2))$`

`$=(8ma^2c)/(h(n_6^2 - n_1^2))$`

`$=(8 * 9.109 * 10^(-31)(0.34 * 10^(-10))^2 (3 * 10^8))/(6.626 * 10^(-34) * (36-1))$`

`$= ( 8 * 9.109 * 0.34 * 0.34 * 3 * 10^(-43))/(6.626 * 35 * 10^(-34))$`

`$=(25.27 * 10^(-43))/(231.91 * 10^(-34))$`

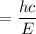
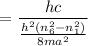
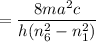
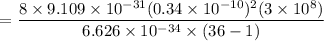
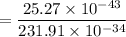
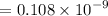`$= 0.108 * 10^(-9)$` m

= 108 pm