Question

If the sum of the even integers between 1 and k, inclusive, is equal to 2k, what is the value of k?

Answer 1

You can make a start by putting together an expression for the sum of the even integers between 1 and k inclusive.

Let S be the sum of the even integers between 1 and k inclusive.

Then:
S=2+4+6+⋯+(k−2)+k

As k is even, you can say r = 2k and so:

S=2(1+2+3+⋯+(r−1)+r)

Now the sum of the first r numbers is well-known, it's the rth triangle number and we have:

1+2+3+⋯+(r−1)+r=r(r+1)/2
Now we can keep it simple and say 2k=4r and so:

S=2(1+2+3+⋯+(r−1)+r)=4r=2r(r+1)2=r(r+1)

So you can build a quadratic in r and so get k.

Answer 2

K = 6

Explanation:

Even integers between 1 and k will be 2, 4, 6, 8, 10.........(k-2), k

Therefore, number of even terms between 1 and k inclusive will be
`(k)/(2)`

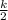
Now we know these even integers will form an arithmetic sequence which has it's first term as 2 and a common difference of 2.

We know sum of an arithmetic sequence is represented by

`S_(n)` =
`(n)/(2)[2a + (n -1)d]`

where a = first term

n = number of therms

d = common difference

2k =
`(k)/(4)[2(2)+((k)/(2)-1)2]`

2k =
`(k)/(4)[4+k-2]`

2k =
`(k)/(4)[k+2]`

8k = k[k + 2]

8 = k + 2

k = 8 - 2

k = 6