Question

Use the following dot plot to determine which statements are true. Select all that apply.

Answer 1

Step 1

Given;

Step 2

We test all the options to know those that apply

`\begin{gathered} 1)\text{ If 7 is deleted from the set, the median will stay the same } \\ The\text{ data written out is; 2,3,3,4,4,4,5,5,5,5,6,6,7} \end{gathered}`

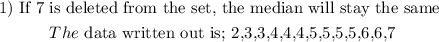
The median of the data is the middle number since the number of data is odd.

`Median=5`

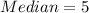
when we remove 7, the data becomes

`\text{ 2,3,3,4,4,4,5,5,5,5,6,6}`

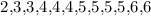
The median now will be;

`(4+5)/(2)=(9)/(2)=4.5`

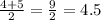
Thus the first option is wrong. If 7 is removed from the set, the median changes.

`\begin{gathered} 2)\text{ About half of the values are greater than the mean.} \\ mean=\frac{sum\text{ of data}}{number\text{ of data}}=(2+3+3+4+4+4+5+5+5+5+6+6+7)/(13) \end{gathered}`
`mean=(59)/(13)`

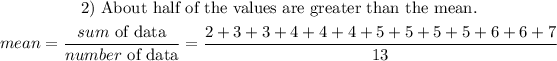
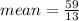
Half of the values will be;

`\begin{gathered} The\text{ data appears evenly skewd} \\ Thus\text{ about half of te values is greater than the mean is correct} \end{gathered}`
`\begin{gathered} If\text{ 2 is deleted from the data set, the median stays the same} \\ 2,\:3,\:3,\:4,\:4,\:4,\:5,\:5,\:5,\:5,\:6,\:6,\:7 \\ If\text{ we remove 2} \\ \:3,\:3,\:4,\:4,\:4,\:5,\:5,\:5,\:5,\:6,\:6,\:7 \end{gathered}`

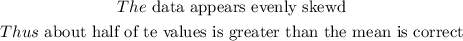
The median will be;

`\begin{gathered} (5+5)/(2)=(10)/(2)=5 \\ The\text{ medain stays the same } \end{gathered}`
`\begin{gathered} If\text{ one of the 5's is deleted from the set, the set becomes bimodal} \\ Bimodal\text{ means two modes} \\ If\text{ we remove one 5} \\ 2,\:3,\:3,\:4,\:4,\:4,\:\:5,\:5,\:5,\:6,\:6,\:7 \\ The\text{ modes are 4 and 5 since they occur highest. 3 times each} \\ Thus,\text{ yes, if one of the 5's is removed from the set, the set becomes bimodal} \end{gathered}`

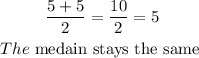
Answer;

About half of the values are greater than the mean.

If 2 is deleted from the set, the median will stay the same.

If one of the 5s is deleted from the set, the set will become bimodal.