Question

Determine the number of real solutions to each quadratic equation 8t^2 - 12t +5=0

Answer 1

We need to determine the number of real solutions to the equation:

`8t^2-12t+5=0`

In order to do so, we can apply the quadratic formula:

`x=(-b\pm√(b^2-4ac))/(2a)`

where a is the constant multiplying x², b is the one multiplying x and c is the independent term.

In this problem, we have:

`\begin{gathered} a=8 \\ b=-12 \\ c=5 \end{gathered}`

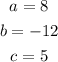
Then, let's use those values to find the number inside the square root. We obtain:

`b^2-4ac=(-12)^2-4(8)(5)=144-160=-16`

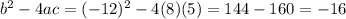
Notice that the term inside the square root is negative. And since the square root of a negative number is an imaginary number, the equation has no real solutions.

Answer: Zero real solutions.