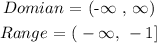Question

Given the functions, complete the sections. a) Find the intercepts with the axes. b) Indicate the basic function that you will use to graph it. c) Identify the transformations that your graph will undergo, starting from its basic function. d) Draw the sketch showing the transformations, taking into account all the previous sections. Highlight f(x) with a pen or marker.e) Determine its domain and range.f(x) = -3x^2 + 12× - 13

Answer 1

Step 1:

Write the function

`f(x)=-3x^2\text{ + 12x - 13}`

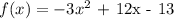
a)

To find the y-intercept, plug x = 0 and to find the x-intercept, plug y = 0

`\begin{gathered} y-\text{intercept} \\ f(0)\text{ = -3}*0^2\text{ + 12(0) - 13 = 0 + 0 - 13 = -13} \\ y-\text{intercept = -13} \\ (\text{ 0, -13 ) y-intercept} \end{gathered}`

b) To graph the function, you will need to find the vertex, the global maximum.

The extreme point is ( 2 , -1 )

Global maximum = ( 2 , -1 )

So you can graph the function using y-intercept (0, -13) and the global maximum (2 , -1)

c)

`\begin{gathered} \text{The basic function of a parabola is } \\ \text{y = x}^2 \end{gathered}`
`\begin{gathered} \text{The graph of a basic function y = x}^2,\text{ undergoes a transformation into } \\ \text{the graph of a function y = -3(x - 2)}^2\text{ - 1} \end{gathered}`

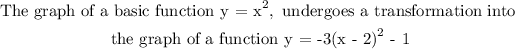
The graph undergoes the following transformation

1. stretched by a factor of 3

`y=3x^2`

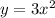
2. Then reflect over the x-axis

`\text{y = -3x}^2`

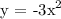
3. Then shift to the right by a factor of 2 units

`\text{y = -3(x - 2)}^2`

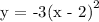
4. The finally shift vertically downward by 1 unit

`\text{y = -3(x - 2)}^2\text{ - 1}`

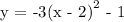
d)

e)

`\begin{gathered} Domian\text{ = (-}\infty\text{ , }\infty) \\ Range\text{ = (}-\infty\text{, }-1\rbrack \end{gathered}`