Question

3 2 5 Evan mixed 2 2/3 pounds of nuts with 1 5/6 pounds of raisins and 1 7/8 pounds of chocolate chips. How many pounds did this mixture weight?

Answer 1

We are told that Evan mixes different amounts of ingredients. The total weight of the mixture is the sum of the weights of each individual ingredient. So we have the following:

2 2/3 pounds of nuts

1 5/6 pounds of raisins and

1 7/8 pounds of chocolate chips.

So we need to do the following operation

`2\text{ }(2)/(3)+1(5)/(6)+1(7)/(8)`

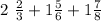
We note that each of this number is a mixed number. So, to add them up, we should first transform each number to its equivalent fraction representation. To do so, we proceed as follows:

1. We identify the whole number of the mixed number. That is, the number that is right next to the fraction.

2. We multiply the whole number from step 1 with the denominator of the fraction.

3. To the result of step 2, we add the numerator.

4. To the result of step 3, we put it on top of the denominator.

So, let us use this procedure and transform the first number 2 2/3

1. The whole number of 2 2/3 is 2.

2. We multiply it by the denominator (3). So we have 2*3 = 6.

3. To 6 we add the numerator (2) so we have 6+2=8.

4. We place 8 on top of the denominator, so we have the following

`2\text{ }(2)/(3)=(8)/(3)`

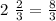
If we repeat this procedure to the other two numbers we get

`1\text{ }(5)/(6)=(11)/(6)`

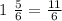
and

`1(7)/(8)=(15)/(8)`

So now, we have to add the following numbers

`(8)/(3)+(11)/(6)+(15)/(8)`

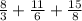
We will first add the first two numbers (from left to right).

Note that

`(8)/(3)=(8)/(3)\cdot(2)/(2)=(16)/(6)`

Then

`(8)/(3)+(11)/(6)=(16)/(6)+(11)/(6)=(27)/(6)=(3\cdot9)/(3\cdot2)=(9)/(2)`

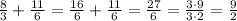
Now, we have to add

`(9)/(2)+(15)/(8)`

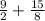
Once again, note that

`(9)/(2)=(9\cdot4)/(2\cdot4)=(36)/(8)`

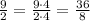
Then

`(9)/(2)+(15)/(8)=(36)/(8)+(15)/(8)=(51)/(8)`

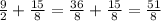
Now we need to transform the fraction to a mixed number. To do so, we proceed as follows:

1. Find a multiple of the denominator that is the closest to the numerator and is less than the numerator. So, in this case we want to find the multiple of 8 that is the closest to 51 and that is also less than 51.

Note that 6*8 =48 and 7*8 = 56. So the closest multiple of 8 that is less than 51 is 48.

2. Write the numerator as the number found in step 1 plus another number.

So, we have that 51 = 48+3. So we have

`(51)/(8)=(48+3)/(8)`

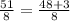
3. Split the sum into to fractions. So

`(48+3)/(8)=(48)/(8)+(3)/(8)`

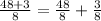
4. Calculate the first division. So

`(48)/(8)+(3)/(8)=6+(3)/(8)`

5. One of the numbers is a whole number and the other is the fraction. So take the whole number as the whole number of the mixed fraction and take the fraction as the mixed fraction. We get

`6+(3)/(8)=6(3)/(8)`

So, the weight of the mixture is

`6(3)/(8)`

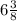
pounds