Let the number of hot dogs sold be represented by h and the number of sodas by s.
Each hot dog costs $3 and each soda costs $2. If $78 is made in total, we have the equation to be:

If a total of 87 hot dogs and sodas combined are sold, we have:
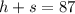
We can rewrite the second equation to give:
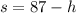
Substituting this value into the first equation, we get:
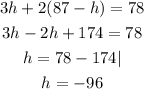
With the calculated value of h, we can get the value of s to be:
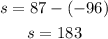
Since a negative value is gotten for the number of hot dogs, it does not represent a real-life scenario.