The given points are A92,4) and B(17,14).
Point P is on the segment AB.
The distance between AB is
![D=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ijelhrk1isbu825y5bor.png)
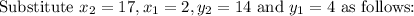
![D=\sqrt[]{(17-2_{})^2+(14_{}-4_{})^2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/j5kd02yp3ignyi5kwsxc.png)
![=\sqrt[]{(15_{})^2+(10)^2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/rusdv01bgbyuax66ngdq.png)
![=\sqrt[]{225+100}=\sqrt[]{325}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/6etswnp1dpaa1dew2ui9.png)
![=\sqrt[]{25*13}=5\sqrt[]{13}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/7mwqm723otvrmny1qscc.png)
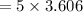
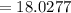
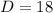
The distance between A and B is 8.
To find the x-coordinate of the point P compute 2/5 of the distance between A and B and add its value to the x-coordinate of A.
The x-coordinate of P is
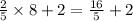
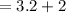
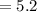
To find the y-coordinate of the point P compute 2/5 of the distance between A and B and add its value to the y-coordinate of A.
The y-coordinate of P is
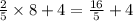
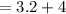
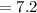
The point P is
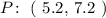
After round the answer, we get point P is (5,7).
Hence the point P is (5,7)