We can list the first four perfect squares:
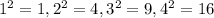
We can following the same pattern to find the rest of the square and compare them to those that are a perfect cube:
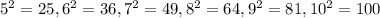
Then, we have
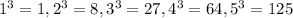
We can see from the two lists:
Perfect squares: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100....
Perfect cubes: 1, 8, 27, 64, 125....
Comparing these two lists, we have that the number 64 is, at the same time, a perfect square and a perfect cube.
Then, to find the answer, we need to make two lists, first, raising the natural numbers to the second power, and then, to the third power, and compare when we get a number is a perfect square and a perfect cube (the other apart from 1).