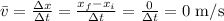ANSWER:
The velocity is 29884.89 m/s
The avergae velocity is 0 m/s
Explanation:
We know that the speed is given by the distance for a certain time (in this case a year).
We know that the distance traveled would be equal to the circumference of the circle formed, which can be calculated by means of the radius.
We have the following equivalences:
1 km = 1000 m
1 year = 365 days
1 day = 24 hours
1 hour = 60 minutes
1 minute = 60 seconds
Therefore, we calculate the velocity as follows:
![\begin{gathered} v=(d)/(t) \\ d=2\cdot\pi\cdot r=2\cdot3.1415\cdot1.5\cdot10^8\operatorname{km}\cdot\frac{1000\text{ m}}{1\text{ km}}=942450000000 \\ t=1\text{ yr}*\frac{365\text{ days}}{1\text{ yr}}*\frac{24\text{ hr}}{1\text{ day}}*\frac{60\text{ min}}{1\text{ hr}}*\frac{60\text{ sec}}{1\text{ min}}=31536000 \\ \text{ replacing} \\ v=(942450000000)/(31536000) \\ v=29884.89\text{ m/s } \end{gathered}]()
Now, since the initial and final position are the same, we would have: