Question

please helpA tourist at scenic Point Loma, California uses a telescope to track a boat approaching the shore. If the boat moves at a rate of10 meters per second, and the lens of the telescope is 45 meters above water level, how fast is the angle of depression of thetelescope changing when the boat is 180 meters from shore? Round any intermediate calculations to no less than sixdecimal places, and round your final answer to four decimal places.

Answer 1

A plot to illustrate the scenario first.

Given the illustration above, our approach is to find the time it will take the plane from the current destination to the place where the telescope is sited.

The boat travels a distance of 180m at 10 metres per second. Therefore, the travel time is:

`t=(180)/(10)=18s`

Having found our time, we now find the angle of depression, D since we have the opposite and adjacent sides.

`\begin{gathered} \tan D=(45)/(180) \\ D=\tan ^(-1)((45)/(180))_{} \\ D=14.036^o \end{gathered}`

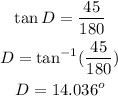
In that case, we can get the rate at which the angle is changing via:

`(14.036)/(18)=0.7798^o\text{per second}`

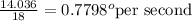
0.7798 degrees per second