Answer:
Part A: 1.47 * 10^ 20 kg
Part B: 5.22 * 10^30 kg.
Step-by-step explanation:
The acceleration due to gravity on a planet of mass M and radius r is given by
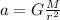
where G = 6.67 *10^-11 m^3 / kg *s^2 = gravitational constant.
Now solving for M gives
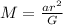
Putting in a = 13.1 m /s^2 and r = (1.5 * 10^9 / 2) gives
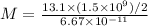
which evaluates to give
![\boxed{M=1.47*10^(20)\operatorname{kg}\text{.}}]()
which is the mass of the planet.
Part B.
Here we use Kepler's third law, which says
![T^2=(4\pi^2)/(GM)a^3]()
where
T = orbital period of the planet
M = mass of the star
a = distance between the star and the planet.
G = gravitational constant
Now solving for M gives
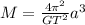
Now putting a = 2.20 * 10^11 , G = 6.67 * 10^-11, and T = 402 * 24 * 60 *60 gives
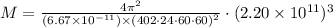
![\boxed{M=5.22*10^(30)\operatorname{kg}\text{.}}]()
Hence, the mass of the star is 5.22 * 10^30 kg.