Question

An object with a mass of 51.40 kg is moving down an inclined plane 32.88° above the horizontal with a net force of -13.89. What is the coefficient of kinetic friction? Hint *** to get the coefficient of kinetic friction you have to solve for the sum of the values

Answer 1

The free body diagram of the object can be shown as,

The net force which acts along the horizontal axis can be expressed as,

`F=mg\sin \theta-\mu N`

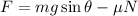
According to free body diagram,

`N=mg\cos \theta`

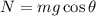
Plug in the known value in the above equation.

`\begin{gathered} F=mg\sin \theta-\mu mg\cos \theta \\ \mu mg\cos \theta=F-mg\sin \theta \\ \mu=(F)/(mg\cos\theta)-(mg\sin \theta)/(mg\cos \theta) \\ =(F)/(mg\cos\theta)-\tan \theta \end{gathered}`

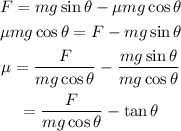
Substitute the known values,

`\begin{gathered} \mu=\frac{-13.89\text{ N}}{(51.40kg)(9.8m/s^2)\cos32.88^(\circ)}(\frac{1kgm/s^2}{1\text{ N}})-\tan 32.88^(\circ) \\ =-(0.028)/(0.84)-0.646 \\ =-0.033-0.646 \\ =-0.679 \end{gathered}`

Thus, the coefficient of kinetic friction is 0.679 and negative sign indicates that the frictional force is in opposite direction of motion of object.