Question

A tree trimmer would like to know how tall a tree is. The treecasts a shadow that is 21 feet long. At the same time, the 5.5ft tall tree trimmer is casting a shadow that is 6 feet long. Howtall is the tree?

Answer 1

The actual height of the tree is 19.25 ft.

Step-by-step explanation:

To determine the height of the tree, we can use the principle of similar triangle;

Let;

St and Sm represent the length of the shadow of the tree and the tree trimmer respectively.

And

Ht and Hm represent the actual height of the tree and the tree trimmer respectively;

Since the two triangles are similar;

`\begin{gathered} (Ht)/(St)=(Hm)/(Sm) \\ Ht=(Hm* St)/(Sm) \end{gathered}`

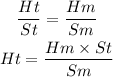
Given;

Hm = 5.5 ft

St = 21 ft

Sm = 6 ft

Substituting the given values we have;

`\begin{gathered} Ht=(5.5*21)/(6) \\ Ht=(115.5)/(6) \\ Ht=19.25\text{ ft} \end{gathered}`

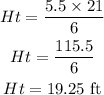
The actual height of the tree is 19.25 ft.