Question

Help with substitution show work please!!!!!!!

Answer 1

Answer: x=4, y=-2

Step-by-step explanation: 4x+y=14, x-2y=8

4x+y-y=14-y

4x/4=14/4-y/4

x=14-y/4-(2y)(4)/4

4(14-9y)/4=(8)(4)

14-9y-14=32-14

-9y/-9=18/-9

y=-2

(14)-(-2)/4

14+2/4

16/4

4

x=4

x=4, y=-2

Answer 2

Solution of given system of equations is: x=4, y=-2 or (4,-2)

Explanation:

Solve the equation using substitution

4x+y=14

x-2y=8

Substitution method involves placing value of x or y from one equation to other equation.

We have

`4x+y=14--eq(1)\\x-2y=8--eq(2)\\`

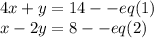
Finding value of x from equation 2

x-2y=8

x=2y+8

Put this value of x in equation 1

`4x+y=14Put\:x=2y+8\\4(2y+8)+y=14\\8y+32+y=14\\9y=14-32\\9y=-18\\y=(-18)/(9)\\y=-2`

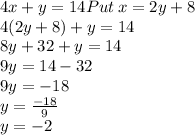
We get y=-2

Now, put value of y into equation 2 to find value of x

`x-2y=8\\x-2(-2)=8\\x+4=8\\x=8-4\\x=4`

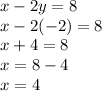
We get x = 4

So, solution of given system of equations is: x=4, y=-2 or (4,-2)