Answer:
The fourth option i.e. 'no solution' is correct.
Explanation:
Given the system of equations
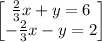
Adding both equations
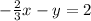

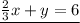
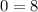
so the system of equations becomes
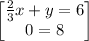
0 = 8 is FALSE!
Therefore, the system of equations has no solution.
Thus,
No Solution!
Hence, the fourth option i.e. 'no solution' is correct.