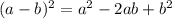Let's understand 4 basic translation rules first:
Let parent function be f(x), so
1. h(x+a) would be f(x) translated a units left
2. h(x-a) would be f(x) translated a units right
3. h(x) + a would be f(x) translated a units up
4. h(x) - a would be f(x) translated a units down
As for reflection, the rules we would need to knw would be:
1. -f(x) would be f(x) replected in x axis
2. f(-x) would be f(x) reflected in y-axis
Now,
given
g is translated 2 units right, that would make f(x):
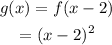
Then,
g is translated 3 units up, so it would be:

Last step is to reflect across y-axis.
This means put "-x" in place of x to get:
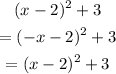
Same thing.
To write the equation in the form wanted, we multiply:
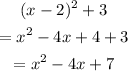
Note: