Question

Barney is an avid coin collector and collects the same number of coins each day. He decides to start keeping better track of his coin collection. After 15 days Barney counts and finds out he has 155 coins. After 22 days he has a total of 218 coins. 1. How many coins is Barney collecting each day? (I think this is 9??)2. Write an equation in point-slope form that represents this situation. 3. After how many days would Barney have 425 coins?

Answer 1

1. How many coins is Barney collecting each day?

To get the average number of coins collected each day, we need to get the different between the number of coins on 22nd day and 15th day over the difference in the number of days. Also, this will be the slope of the equation.

`\text{slope}=(218-155)/(22-15)=(63)/(7)=9`

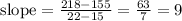
Hence, Barney is collecting an average of 9 coins every day.

2. Based on the situatuon, we have two points here. Assuming x = number of days and y = number of coins collected, the coordinates of the two points are (15, 155) and (22, 218).

We can determine the equation using the two-point form of the equation then, we'll convert it to point-slope form.

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

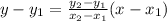
where (x₁, y₁) is our first point that is (15, 155) and (x₂, y₂) is our second point at (22, 218). Let's plug this in to the formula above.

`y-155=(218-155)/(22-15)(x-15)`

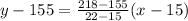
Then, convert it to point-slope form by solving the slope.

`\begin{gathered} y-155=(63)/(7)(x-15) \\ y-155=9(x-15) \end{gathered}`

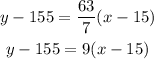
The equation in point-slope form is y - 155 = 9(x - 15).

3. Since we have stated in number 2 that y = number of coins collected, we are goind to assume that y = 425 coins. Let's plug it in to the equation above to solve for x or the number of days.

`\begin{gathered} 425-155=9(x-15) \\ 270=9x-135 \\ \text{Add 135 on both sides.} \\ 405=9x \\ \text{Divide 9 on both sides.} \\ 45=x \end{gathered}`

Therefore, after 45 days, Barney will have collected 425 coins.