Question

In a parallelogram ABCD, the length of the longer arm is equal to twice the length of the shorter arm....

Answer 1

C. 12m

Explanation:

Let the length of the shorter arm = x

Since the length of the longer arm is equal to twice the length of the shorter arm;

• The length of the longer arm = 2x

• The area of triangle ABD = 18√3 m².

Given a triangle with two sides and the included angle, the area of the triangle is calculated using the formula below:

`\begin{gathered} \text{Area}=(1)/(2)ab\sin \theta \\ \implies\text{Area of triangle ABD =}(1)/(2)bd\sin A \end{gathered}`

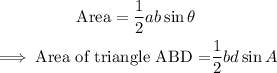
Therefore:

`18\sqrt[]{3}=(1)/(2)(x)(2x)\sin (60\degree)`

We solve for x.

`\begin{gathered} 18\sqrt[]{3}=(2x^2)/(2)*\sin 60\degree \\ 18\sqrt[]{3}=x^2*\frac{\sqrt[]{3}}{2} \\ \text{Multiply both sides by }\frac{2}{\sqrt[]{3}} \\ 18\sqrt[]{3}*\frac{2}{\sqrt[]{3}}=x^2*\frac{\sqrt[]{3}}{2}*\frac{2}{\sqrt[]{3}} \\ x^2=36 \\ x^2=6^2 \\ x=6 \end{gathered}`

Multiply x by 2 to get the length of the longer arm:

`2x=2*6=12m`

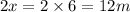
The length of the longer arm is 12m.

C is the correct option.