Question

find the volume of the figure below. as you can tell my teacher has already given me the answers she wants me to show how she got the answers.

Answer 1

byIf we take a look at the given figure, there are two parts present on it, one is a rectangular prism and one is a semi-circle with a given thickness.

In the given problem, the width of the rectangular prism is equal to 7 cm, its length is equal to 12 cm, and its thickness is equal to 5 cm. Hence, the volume of the rectangular prism part of the figure is equal to

For the semi-circle part of the problem, we want to take a look first at the area of the semi-circle. If a full circle has an area given by the equation

`A_(circle)=\pi* r^2`

The area of a semi-circle is just the half of the area of the full circle, hence,

`A_(semi-circle)=\frac{\pi* r^2^{}}{2}`

We want to look at the radius of the semi-circle. The rectangular prism has a width of 7 cm, which corresponds to the diameter of the semi-circle. Therefore, its radius is just half of the diameter, which is equal to 3.5 cm. Solving for the area of the semi-circle, we have

`A_(semi-circle)=(\pi*3.5^2)/(2)=19.24cm^2`

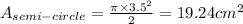
Now, for the volume of the semi-circle, let's just multiply the area of the semi-circle to the thickness of the semi-circle, hence, its volume is equal to

`V_(semi-circle)=(19.24cm^2)*(5cm)=96.2cm^3`

Finally, the total volume is just the sum of the volume of the semi-circle and the rectangular prism. We have

`V_(tot)=420cm^3+96.2cm^3=516.2cm^3`

Which is the same as the provided answer on the question tab.