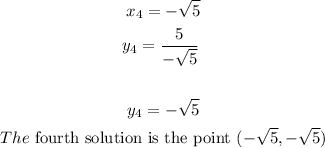Question

Solve by substitution.
`xy = 5 \\ {5x}^(2) + {y}^(2)`

Answer 1

we have the system of equations

`\begin{gathered} xy=5 \\ y=(5)/(x)\text{ ----> equation 1} \\ 5x^2+y^2=30\text{ ----> equation 2} \\ \end{gathered}`

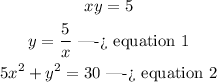
Solve by substitution

substitute equation 1 in equation 2

`5x^2+((5)/(x))^2=30`

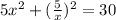
solve for x

`\begin{gathered} 5x^2+(25)/(x^2)=30 \\ (5x^4+25)/(x^2)=30 \\ \\ 5x^4+25=30x^2 \\ 5x^4-30x^2+25=0 \\ \end{gathered}`

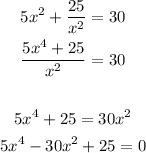
Let

change of variable

`\begin{gathered} u^2=x^4 \\ u=x^2 \end{gathered}`

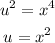
substitute

`\begin{gathered} 5x^4-30x^2+25=0 \\ 5u^2-30u+25=0 \end{gathered}`

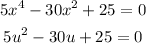
Solve the quadratic equation

using the formula

a=5

b=-30

c=25

substitute

`u=(-(-30)\pm√(-30^2-4(5)(25)))/(2(5))`
`u=(30\pm20)/(10)`

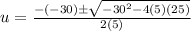
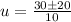
The values of u are

u=5 and u=1

Now solve for x

Remember that

`\begin{gathered} u=x^(2) \\ For\text{ u=1} \\ x^2=1 \\ x_1=1 \\ x_2=-1 \\ For\text{ u=5} \\ x^2=5 \\ x_3=√(5) \\ x_4=-√(5) \end{gathered}`

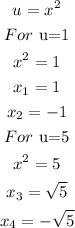
Find out the values of y

For each value of x find out the value of y

Remember that

`\begin{equation*} y=(5)/(x)\text{ } \end{equation*}`

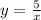
For x_1

`\begin{gathered} x_1=1 \\ y_1=(5)/(1)=5 \end{gathered}`

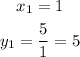
The first solution is the point (1,5)

For x_2

`\begin{gathered} x_2=-1 \\ y_2=(5)/(-1)\text{ =-5} \end{gathered}`

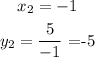
The second solution is the point (-1,-5)

For x_3

`\begin{gathered} x_3=√(5) \\ y_3=(5)/(√(5))\text{ } \\ \\ y_3=√(5) \\ The\text{ third solution is the point \lparen}√(5),√(5)) \end{gathered}`

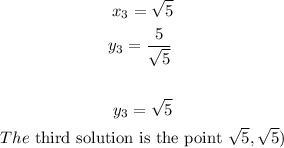
For x_4

`\begin{gathered} x_4=-√(5) \\ y_4=(5)/(-√(5))\text{ } \\ \\ y_4=-√(5) \\ The\text{ fourth solution is the point }(-√(5),-√(5)) \end{gathered}`