Question

Suppose the area of a rectangle is 1023 +37x2 + 38x + 20 and the length is 2x + 5. What is the width of the rectangle?Width:

Answer 1

Step-by-step explanation

Let's picture the situation of the exercise:

We're looking for the width of the above rectangle. Recall that the area of a rectangle is given by the following equation:

`A=L\cdot W\leftarrow\begin{cases}A=area, \\ L=\text{length,} \\ W=\text{width.}\end{cases}`

For our rectangle, this equation looks like

`10x^3+37x^2+38x+20=(2x+5)\cdot W\text{.}`

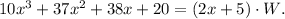
Solving this equation for W, we get

`W=(10x^3+37x^2+38x+20)/(2x+5)\text{.}`

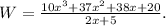
Then, the exercise turns out to be a polynomial division. let's do it:

Then,

`(10x^3+37x^2+38x+20)/(2x+5)=\text{ Quotient}+\text{ Residue}=(5x^2+6x+4)+0=5x^2+6x+4.`

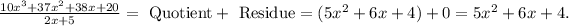
And Thus,

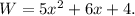
`W=5x^2+6x+4.`Answer

The width of the given rectangle is

`5x^2+6x+4.`