Question

What do you know about a quadratic equation that has the following points (2, 0) and (10, 0)?A. The parabola must open up.B. The parabola will have a negative y-intercept.C. The x-coordinate of the vertex must be 6.D. The graph must be wider than the parent function.

Answer 1

Step-by-step explanation

The equation of a parabola can be written in its factored form like this:

`a(x-r_1)(x-r_2)`

Where a is a number known as the leading coeffcient and the r's are the roots or zeros of the function i.e. the x-values for which the function is equal to 0. At this x-values the parabola intercepts the x-axis so we know that it passes through the points:

`(r_1,0),(r_2,0)`

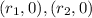
The leading coefficient a defines if the parabola opens up (a>0) or down (a<0) and if it's wider (|a|>1) or narrower (|a|<1) than the parent function x².

The question tells us that we only know that the parabola of the equation passes through (2,0) and (10,0). This implies that x=2 and x=10 are zeros of the parabola because the two points mentioned are in the x-axis. Then what we know about this equation is that is factored form looks like this:

`a(x-2)(x-10)`

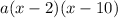
So "a" can take any value. Then we can't assure if the parabola opens up or down or if it's wider or narrower than the parent function so we can discard options A and D.

Now let's see what happens with the y-intercept. At the y-intercept the value of x is 0 so let's replace x with 0 in the factored form and see if the result is positive or negative:

`a(0-2)(0-10)=a\cdot(-2)\cdot(-10)=20a`

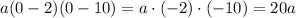
But "a" can take any value which means that we don't know if the y-intercept is negative or positive so we can discard option B.

The x-coordinate of the vertex is the midvalue between the zeros. Since the zeros are x=2 and x=10 this midvalue is:

`(2+10)/(2)=(12)/(2)=6`

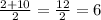
So the x-coordinate of the vertex is 6.

Answer

Since options A, B and D are discarded and C was proved we have that the answer is option C.