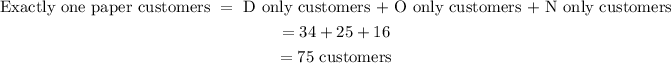Question

A newspaper vendor sells three papers to 135 customers, the papers are the daily times, the observer and the new Nigeria. 70 customers buy the daily time, 60 the observer, 50 the new Nigeria, 17 buy both the daily times and the observer, 15 buy both the observer and the new time Nigeria, 16 the daily times and new Nigeria. How many customers bought(1) The new Nigeria only (2) The observer only (3) Daily Times only (4) Exactly Two papers (5) Exactly One paper

Answer 1

1. 16 customers bought the New Nigeria only

2. 25 customers bought the Observer only

3. 34 customers bought the Daily Times only

4. 39 customers bought exactly two papers

5. 75 customers bought exactly one paper

Step-by-step explanation:

Let D represent the Daily Times newspapers, O represent the Observer newspapers and N represent the New Nigeria newspapers.

From the question, we're given the following;

*Total number of customers, n(D U O U N) = 135

*Number of customers that bought the Daily Times, n(D) = 70

*Number of customers that bought the Observer, n(O) = 60

*Number of customers that bought the New Nigeria, n(N) = 50

*Number of customers that bought both Daily Times and the Observer, n(D n O) = 17

*Number of customers that bought both the Observer and the New Nigeria, n(O n N) = 15

*Number of customers that bought both Daily Times and the New Nigeria, n(D n N) = 16

Let's determine how many customers bought all three papers using the below formula;

`n(D\cup O\cup N)=n(D)+n(O)+n(N)-n(D\cap O)-n(D\cap N)-n(O\cap N)+n(D\cap O\cap N)`
`\begin{gathered} 135=70+60+50-17-16-15+n(D\cap O\cap N) \\ n(D\cap O\cap N)=135-132 \\ n(D\cap O\cap N)=3 \end{gathered}`

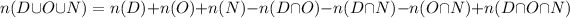
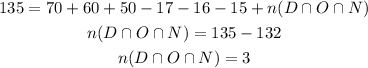
We can see from the above that only 3 customers bought all 3 papers.

1. Let's go ahead and determine how many customers bought only New Nigeria as seen below;

`\begin{gathered} N\text{ only}=n(N)-n(O\cap N)-n(D\cap N)-n(D\cap O\cap N) \\ =50-15-16-3 \\ =16\text{ customers} \end{gathered}`

2. Let's go ahead and determine how many customers bought only Observer as seen below;

`\begin{gathered} O\text{ only}=n(O)-n(D\cap O)-n(O\cap N)-n(D\cap O\cap N) \\ =60-17-15-3 \\ =25\text{ customers} \end{gathered}`

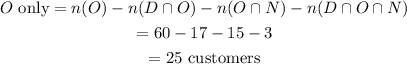
3. Let's go ahead and determine how many customers bought only Daily Times as seen below;

`\begin{gathered} D\text{ only}=n(D)-n(D\cap O)-n(D\cap N)-n(D\cap O\cap N) \\ =70-17-16-3 \\ =34\text{ customers} \end{gathered}`

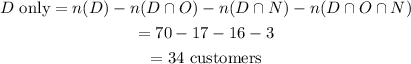
4. Let's now determine the number of customers that bought exactly two papers;

`\begin{gathered} D\text{ and O only}=n(D\cap O)-n(D\cap O\cap N)=17-3=14\text{ customers} \\ O\text{ and N only }=n(O\cap N)-n(D\cap O\cap N)=15-3=12\text{ customers} \\ D\text{ and N only }=n(D\cap N)-n(D\cap O\cap N)=16-3=13\text{ customers} \\ \therefore\text{Exactly Two papers customers }=14+12+13=39\text{ customers} \end{gathered}`

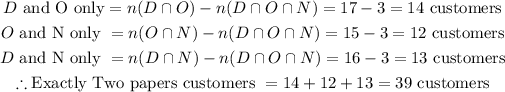
5. Let's now determine the number of customers that bought exactly one paper;

`\begin{gathered} \text{Exactly one paper customers }=\text{ D only customers + O only customers + N only customers} \\ =34+25+16 \\ =75\text{ customers} \end{gathered}`