To solve the exercise, first replace the value of y of the line in the equation of the circle, like this
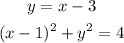
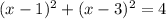
Solving for x you have
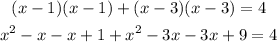
Subtract 4 from both of the equation and operate like terms
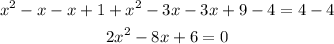
Now you can use the general formula for quadratic equations, that is
![\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/akuf1apf9if6mr85rckz.png)
In this case
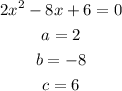
So, you have
![\begin{gathered} x=\frac{-(-8)\pm\sqrt[]{(-8)^2-4(2)(6)}}{2(2)} \\ x=\frac{8\pm\sqrt[]{64-48}}{4} \\ x=\frac{8\pm\sqrt[]{16}}{4} \\ x=(8\pm4)/(4) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/c7qoqi13kz0odn2gfqvj.png)
Then the solutions of the quadratic equation will be
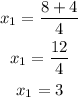
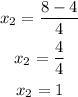
Finally, to get the y-coordinate of the intersection points between the line and the circle, replace the values of x found in any of the initial equations, for example in the equation of the line
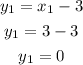
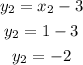
Therefore, the points where the line and the circle intersect are
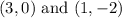
And the correct answers are E. and C.