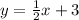
Step-by-step explanation
Sep 1
Find the first derivative of f(x)
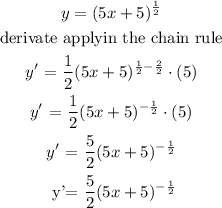
Step 2
Plug x value of the indicated point into f '(x) to find the slope at x.
so
Therefore, at x = 4, the slope of the tangent line is
![\begin{gathered} \text{ y'= }(5)/(2)(5(4)+5)^{-(1)/(2)} \\ \text{ y'= }(5)/(2)(25)^{-(1)/(2)} \\ \text{ y'= }(5)/(2)\cdot\frac{1}{\sqrt[]{25}} \\ \text{ y'= }(5)/(2)\cdot(1)/(5)=(1)/(2) \\ so,\text{ the slope is 1/2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/bj4kqg0wwp59benbm4gk.png)
Step 3
finally, find the equation of the lne by using

so, the answer is
I hope this helps you