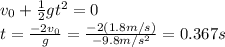Answer:
0.367 s
Step-by-step explanation:
Tina has a unifomrly accelerated motion along the vertical direction, with initial velocity
 and constant acceleration
and constant acceleration
 downward (acceleration due to gravity). Its position at time t is given by the equation:
downward (acceleration due to gravity). Its position at time t is given by the equation:
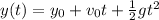
where
 is the initial height, so we can remove it from the equation:
is the initial height, so we can remove it from the equation:

We need to find how long is Tina in the air, which means we have to find the time t at which Tina reaches the ground again, so the time t at which
 :
:
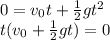
which has two solutions:
 --> time at which Tina starts its motion, so we don't consider this one
--> time at which Tina starts its motion, so we don't consider this one