Question

7.50L of a gas was at an unknown pressure.However at standard pressure,it's volume was measured to be 8.00L what was the unknown pressure

Answer 1

The standard pressure is a value that was standardized by us.

It was 1 atm until 1982, but it changed to 1 bar since then.

Sice some still use the old one, I will answer using both.

In the case of the old standard, the pressure is:

`p=1atm`

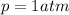
We know that the volume at the standard pressure is 8.00 L.

If we ssume that the gas behaves as an ideal gas, we can use the Boyle's Law, which says that, for constant temperature:

`pV=k`

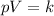
Where k is constant.

So, in the first case, we have:

`\begin{gathered} V_1=7.50L \\ p_1=? \end{gathered}`

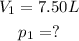
And in the second case we have:

`\begin{gathered} V_2=8.00L \\ p_2=1atm \end{gathered}`

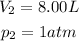
So, using the Boyle's Law:

`\begin{gathered} p_1V_1=k \\ p_2V_2=k \\ p_1V_1=p_2V_2 \\ p_1=(p_2V_2)/(V_1)=(1atm\cdot8.00L)/(7.50L)=1.0666\ldots atm\approx1.07atm \end{gathered}`

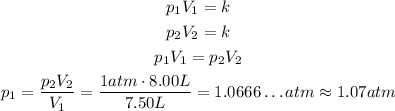
If we consider the new standard pressure, then the only difference is that:

`p_2=1bar`

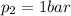
The other values are the same, so we have, in the first case:

`\begin{gathered} V_1=7.50L \\ p_1=? \end{gathered}`

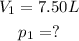
And, in the second case:

`\begin{gathered} V_2=8.00L \\ p_2=1atm \end{gathered}`

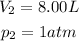
So, applying the Boyle's Law:

`\begin{gathered} p_1V_1=k \\ p_2V_2=k \\ p_1V_1=p_2V_2 \\ p_1=(p_2V_2)/(V_1)=(1bar\cdot8.00L)/(7.50L)=1.0666\ldots bar\approx1.07bar \end{gathered}`

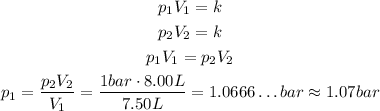
The answer is then:

For the old standard pressure of 1 atm: the unknown pressure is approximately 1.07 atm.

For the new standard pressure of 1 bar: the unknown pressure is approximately 1.07 bar.