Question

Find the ratio of the diameter of aluminum to silver wire, if they have the same resistance per unit length (as they might in household wiring).dAl/dAg =

Answer 1

Given:

The resistance per unit length of aluminum is equal to the resistance per unit length of silver i.e.,

`(R_(Al))/(l_(Al))=(R_(Ag))/(l_(Ag))`

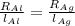
Required: The ratio

`(d_(Al))/(d_(Ag))`

Step-by-step explanation:

The resistance of aluminum is given by the formula

`\begin{gathered} R_(Al)=\rho_(Al)(l_(Al))/(A_(Al)) \\ (R_(Al))/(l_(Al))=(\rho_(Al))/(\pi(r_(Al))^2) \\ (R_(Al))/(l_(Al))=(\rho_(Al))/(\pi((d_(Al))/(2))^2) \end{gathered}`

The resistance of silver is given by the formula

`\begin{gathered} R_(Ag)=\rho_(Ag)(l_(Ag))/(A_(Ag)) \\ (R_(Ag))/(l_(Ag))=(\rho_(Ag))/(\pi(r_(Ag))^2) \\ (R_(Ag))/(l_(Ag))=(\rho_(Ag))/(\pi((d_(Ag))\/2)^2) \end{gathered}`

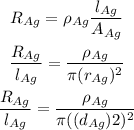
Since,

`(R_(Al))/(l_(Al))=(R_(Ag))/(l_(Ag))`

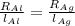
On substituting the values, the ratio can be calculated as

`\begin{gathered} (\rho_(Al))/(\pi((d_(Al))/(2))^(2))=(\rho_(Ag))/(\pi(((d_(Ag)))/(2))^(2)) \\ (\rho_(Al))/((d_(Al))^2)=(\rho_(Ag))/((d_(Ag))^2) \\ ((d_(Al))^2)/((d_(Ag))^2)=(\rho_(Al))/(\rho_(Ag)) \\ (d_(Al))/(d_(Ag))=\sqrt{(\rho_(Al))/(\rho_(Ag))} \end{gathered}`

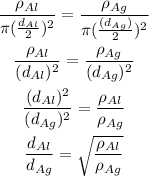
Thus, the ratio is

`(d_(Al))/(d_(Ag))=\sqrt{(\rho_(Al))/(\rho_(Ag))}`

Final Answer: The ratio of the diameter of aluminum to silver is the square root of the ratio of resistivity of aluminum to silver.