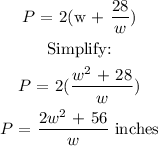Question

A rectangle has an area of 28 square inches. Let w denote the width in inches of the rectangle.(a) Express the height of the rectangle in terms of w.h =(b) Express the perimeter of the rectangle in terms of w.P=

Answer 1

(a) h = 28/w

`(b)\text{ }P\text{ = }\frac{2w^2\text{ + 56}}{w}\text{ inches}`

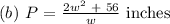
Step-by-step explanation

We have that the Area of the rectange is given as 28 square inches.

We know that the area of a rectangle is found by using:

A = w * h

where w = width, h = height.

Therefore, we have that:

28 = w * h

(a) To express the height in terms of width, we simply make h the subject of the formula above:

`h\text{ = }(28)/(w)`

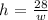
(b) The perimeter of a rectangle is given as:

P = 2(w + h)

Now, put h as 28/w:

`\begin{gathered} P\text{ = 2(w + }(28)/(w)) \\ \text{Simplify:} \\ P\text{ = 2(}\frac{w^2\text{ + 28}}{w}) \\ P\text{ = }\frac{2w^2\text{ + 56}}{w}\text{ inches} \end{gathered}`