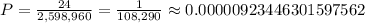Question

24. Compute the probability of randomly drawing five cards from a deck and getting 3 Aces and 2 Kings.

Answer 1

To compute this probability, we will have to compute how many outcomes are possible for five draws from a deck and how many of these have exactly 3 aces and 2 kings.

Assuming it is a standard deck of 52 cards, we have a total of 4 aces and 4 kings in the deck.

This means that we need to calculate the combinations in two groups and then combine these groups.

The first group are the 3 aces. Since the order doesn't matter, we have a case of "4 choose 3":

`C_1=(4!)/(3!(4-3)!)=(4!)/(3!)=4_{}`

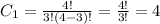
The other group are the kings, but we will pick only 2, so it is "4 choose 2":

`C_2=(4!)/(2!(4-2)!)=(4!)/(2!2!)=3\cdot2=6`

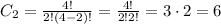
Now, we want to combine these two groups, we do it by multiplying their possible combinations:

`C=4\cdot6=24`

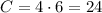
So, there are 12 possible hands with 3 aces and 2 kings.

Now, we ned to compute the total possible outcomes. Since we have a deck of 52 cards and will pick 5, this is "52 choose 5":

`C_a=(52!)/(5!(52-5)!)=(52!)/(5!47!)=(52\cdot51\cdot50\cdot49\cdot48)/(5\cdot4\cdot3\cdot2\cdot1)=(52\cdot17\cdot5\cdot49\cdot12)/(1\cdot1\cdot1\cdot1\cdot1)=2,598,960`

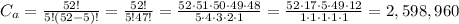
Then the probability will be the combinations of the hand we want over the total combinations:

`P=(24)/(2,598,960)=(1)/(108,290)\approx0.00000923446301597562`