Solving an equation by completing the square
Having the following equation:
-4x² + 32x - 60 = 0
we want to solve it
Step 1: we divide both sides by -4
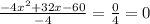
we distribute the division for each term
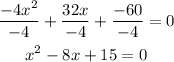
Step 2: completing the square
We want to transform the left side to the form:
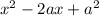
We are going to rearrange our equation so we have just the first and second term, in order to do so we substract 15 both sides:

We want to express the second term, 8x, as a multiplication by 2, 2a. Since
2 · 4 = 8, then we have that a = 4.
Then
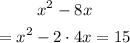
Since a² = 4² = 16, we are going to add both sides 16, so we have this equation with the form of the beggining of this step:
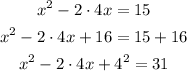
Step 3: solving the equation
We are going to factor the left side of the equation:
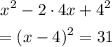
Now, we square root both sides:
![\begin{gathered} (x-4)^2=31 \\ x-4=\pm\sqrt[]{31} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/w663raqt456qv43i7o8l.png)
Now, we add 4 both sides:
![x^{}=4\pm\sqrt[]{31}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/n1sx01ihdvyzfy3k65rz.png)
We have two answers now,
![\begin{gathered} x_1=4+√(31)\approx4+5.6=9.6 \\ x_2=4-\sqrt[]{31}\approx4-5.6=-1.6 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/eok31riaahvlxn61i33h.png)