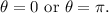Question

The difference in length of a spring on a pogo stick from its non-compressed length when a teenager is jumping on it after θ seconds can be described by the function f of theta equals 2 times cosine theta plus radical 3 period If the angle was doubled, that is θ became 2θ, what are the solutions in the interval [0, 2π)? How do these compare to the original function?

Answer 1

Part A.

The length of the non-compressed spring can be determined by setting

`\theta=0.`

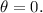
Now, evaluating the given function at θ=0, we get:

`f(0)=2\cos (0)+\sqrt[]{3}.`

Recall that:

`\cos 0=1.`

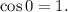
Therefore:

`f(0)=2\cdot1+\sqrt[]{3}=2+\sqrt[]{3.}`

Now, to determine all the possible times at which the length will be equal to the non-compressed length, we set the following equation:

`2\cos \theta+\sqrt[]{3}=2+\sqrt[]{3}.`

Solving the above equation for θ, we get:

`\begin{gathered} 2\cos \theta=2, \\ \cos \theta=1. \end{gathered}`

The solutions to the above equation are:

`\theta=2n\pi,\text{ where n is a natural number or zero.}`

Answer part A:

`\theta=2n\pi,\text{ where n is a natural number or zero.}`

Part B: If we set θ to the double of itself, then, the solutions to the following equation

`f(2\theta)=2+\sqrt[]{3},`

are:

`2\theta=2n\pi,`

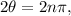
therefore:

`\theta=n\pi,\text{ where n is a whole number.}`

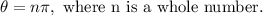
If

`\theta\in\lbrack0,2\pi),`

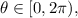
then

`\theta=0\text{ or }\theta=\pi.`

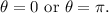
Answer part B: The difference is that the period is half of the original period.

`\theta=0\text{ or }\theta=\pi.`