Question

Consider the function y=4x2+8x−31.(a) Give the coordinates of the vertex of the graph of the function.(b) Graph the function on a window that includes the vertex.

Answer 1

Given the following function:

`\text{ y = 4x}^2\text{ + 8x - 31}`

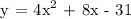
​(a) Give the coordinates of the vertex of the graph of the function.

First, let's identify the value of a, b and c.

`\text{ y = ax}^2\text{ + bx + c}`

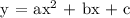
We get,

a = 4

b = 8

c = -31

Let's first the x-coordinate of the vertex.

`\text{ x = }\frac{\text{ -b}}{\text{ 2a}}`
`\text{ = }\frac{\text{ -(8)}}{\text{ 2(4)}}\text{ = }\frac{\text{ -8}}{\text{ 8}}`
`\text{ x = -1}`

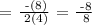
Next, let's find the y-coordinate of the vertex. Substitute x = -1 to the given function.

`\text{ y = 4x}^2\text{ + 8x - 31}`
`\text{ = 4(-1)}^2\text{ + 8(-1) - 31 = 4(1) - 8 - 31}`
`\text{ = -4 - 31}`
`\text{ y = -35}`

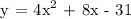
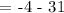
Therefore, the vertex of the graph of the function is at the point -1, -35

Answer: -1, -35

Plotting this into a graph, we get: