Question

Dylan is deciding between two different movie streaming sites to subscribe to. Plan Acosts $16 per month plus $2 per movie watched. Plan B costs $12 per month plus $3per movie watched. Let A represent the monthly cost of Plan A if Dylan watches Iper month, and let B represent the monthly cost of Plan B if Dylan watches x moviesper month. Graph each function and determine the number of monthly movieswatched, x, that would make the two plans have an equal monthly cost.I already tried to solve this but I got it incorrect and I have one more try at it and not sure how to get the final answer. what i have attached is what i have rn.

Answer 1

"y" will represent the total cost per month

"x" will represent the number of movies watched in one month

There are two streaming plans:

Plan A

Has a monthly fee of $16 plus $2 per movie watched.

→ So if he watches no movies in a month, he will pay $16 and for each movie watched he will pay an extra $2

You can represent the monthly cost of plan A as follows:

`y=16+2x`

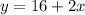
Plan B

Has a monthly fee of $12 plus $3 for every movie watched.

The monthly cost of the plan can be expressed as follows:

`y=12+3x`

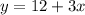
For both equations the y-interceot represents the monthly fee of the plan and the slope of the line is the cost per movie.

To determine the number of movies (x) that would make both plans cost the same for one month using a graph, you have to draw both lines and determine the point where they intercept. The x-coordinate of said point will be the number of movies that make both plans cost the same.

To draw the lines you have to determine at least two points of the line.

The easiest point will be the y-intercept, for the second point, choose any value of x, replace it in the formula and calculate the corresponding value of y. Then plot both points and draw the line.

For plan A

`y=16+2x`

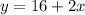
y-intercept, x=0

`\begin{gathered} y=16+2\cdot0 \\ y=16 \end{gathered}`

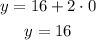
The coordinates are (0,16)

Second point, for example, for x= 2 movies

`\begin{gathered} y=16+2\cdot2 \\ y=16+4 \\ y=20 \end{gathered}`

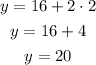
The coordinates are (2,20)

For plan B

y-intercept, x=0

`\begin{gathered} y=12+3\cdot0 \\ y=12 \end{gathered}`

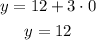
The coordinates are (0,12)

Second point, for example, for x=3

`\begin{gathered} y=12+3\cdot3 \\ y=12+9 \\ y=21 \end{gathered}`

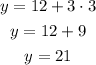
The coordinates are (3,21)

The red line represents the cost with respect to the number of movies for plan A

The purple line represents the cost with respect to the number of movies for plan B

Where both lines intercept indicates the point when both plans cost the same. Said point is (4,24), which means that when you watch x=4 movies both plans will cost $24 that month.