Question

A publisher wants to estimate the mean length of time (in minutes) all adults spend reading newspapers. To determine this estimate, the publisher takes a random sample of 15 people and obtains the following results. 11, 9, 8, 10, 10, 9, 7, 11, 11, 7, 6, 9, 10, 8, 10. From past studies, the publisher assumes σ is 1.5 minutes and that the population of times is normally distributed. The 90% confidence interval for μ is ____________. (Sample mean = 9.1) hn

Answer 1

Sample Size (n) = 15

Samples: 11, 9, 8, 10, 10, 9, 7, 11, 11, 7, 6, 9, 10, 8, 10

Standard Deviation (σ) = 1.5 mins

Mean = 9.1

Normally Distributed

Let's go ahead and solve now the confidence interval. Here are the steps.

1. Subtract the confidence interval from 1 and then divide the result by two.

`(1-0.90)/(2)=(.10)/(2)=0.05`

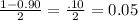
2. Subtract the result (0.05) from 1 and then look up the area in the z-distribution.

`\begin{gathered} 1-0.05=0.95 \\ \end{gathered}`

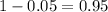
Looking at the z-table, the z-score that has a value of 0.95 is 1.645.

3. Use this formula and apply the given values that we got (z-value, sample size, and standard deviation).

`\begin{gathered} =z*\frac{\sigma}{\sqrt[]{n}} \\ =1.645*\frac{1.5}{\sqrt[]{15}} \\ =1.645*0.3872983346 \\ =0.6371 \end{gathered}`

4. We will add and subtract the resulting value in number 3 to the mean of our sample. The mean given is 9.1

`\begin{gathered} 9.1-0.6371=8.46\approx8.5 \\ 9.1+0.6371=9.74\approx9.7 \end{gathered}`

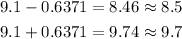
Therefore, the confidence interval is (8.5, 9.7). It is Option 1.