Question

A 0.1 kg mass hangs vertically in equilibrium. In this position, the spring is extended 0.05 m beyond it's un-stretched length. The spring is then stretched an additional 0.05 m and released. What is the total energy in the oscillator?

Answer 1

0.0245 J

Step-by-step explanation

Given:

• The mass of the hanging object, m = 0.1 kg

,

• The extension of the spring when the mass is in equilibrium, x₁ = 0.05 m

,

• The additional extension of the spring, x₂ = 0.05 m

Find:

• The total energy in the oscillator, E

First, we have to find what is the spring constant. We can do this by applying Newton's second law of motion when the mass is in equilibrium,

The spring force and the weight of the mass, when it is in equilibrium, are equal in magnitude,

`F_s=F_g`

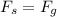
The definition of each force is,

`k\Delta x=mg`

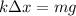
Where k is the spring constant and Δx = x₁. Solving for k,

`k=(mg)/(x_1)=(0.1kg\cdot9.8m/s^2)/(0.05m)=19.6kg/s^2`

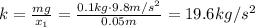
Now, we can find the total energy of the oscillator, which is given by,

`E=(1)/(2)kA^2`

Where k is the spring constant and A is the amplitude of the oscillation - in this case, this is how much the spring is stretched from the un-stretched length, so A = 0.05 m,

`E=(1)/(2)\cdot19.6kg/s^2\cdot0.05^2m^2=0.0245\text{ }J`

Hence, the total energy in the oscillator is 0.0245 Joules.