Question

A small motorboat travels 12 mph in still water. It takes 1 hour longer to travel 64 miles going upstream than it does going downstream. Find the rate of the current.(Hint: 12 + x = rate going downstream and 12 - x = rate going upstream)(Round your answer to the nearest tenth.)AnswerHow to enter your answer (Opens in new window)EKeypad

Answer 1

We will have the following:

First, we recall that velocity times time is distance, so the following is true:

*Downstream:

`(12mph+x)t=64mi`

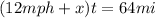
*Upstream:

`(12mph-x)(t+1)=64mi`

Now, we solve for "t" in both:

**Downstream:

`t=(64)/(12+x)`

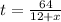
**Upstream:

`t=(64)/(12-x)-1`

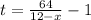
Now, we equal both expressions and solve for "x", that is:

`\begin{gathered} (64)/(12+x)=(64)/(12-x)-1\Rightarrow(64)/(12+x)=(-x-52)/(x-12) \\ \\ \Rightarrow64(x-12)=(-x-52)(x+12)\Rightarrow64x-768=-x^2-64x-624 \\ \\ \Rightarrow x^2+128x-144=0\Rightarrow x=(-(128)\pm√((128)^2-4(1)(-144)))/(2(1)) \\ \\ x=4√(265)-64\Rightarrow x\approx1.1 \\ x=-4√(265)-64\Rightarrow x\approx-129.1 \end{gathered}`

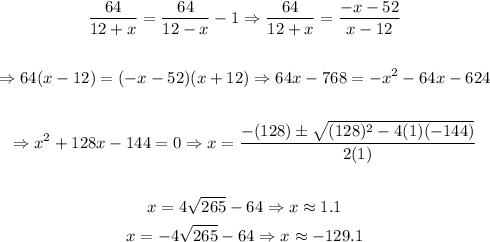
Now, since a negative value for the expressions written won't make much sense [Due to the formulation of the problem], we will have that the speed of the current is approximately 1.1 mph.