Question

f(x) = 6x2 +10- 1what is that value of the discriminant of f ?how many district real number zeros does f have ?

Answer 1

To find the discriminant of this quadratic expression, we need to use part of the quadratic formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

The discriminant is the part of the formula under the radical symbol. We have that the values for a, b and c are given by:

`ax^2+bx+c=0`

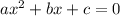
Then, considering the quadratic function in question we have:

`f(x)=6x^2+10x-1=0`

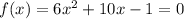
The solutions for this equation are the roots or zeroes of the function.

Thus:

a = 6

b = 10

c = -1

The discriminant of the function is:

`D=b^2-4ac`

Then, using the discriminant of the quadratic formula, we have:

`b^2-4ac\Rightarrow10^2-4(6)(-1)=100+24=124`

We have that:

1. If the discriminant is greater than zero (D > 0), the parabola (the function) will have two x-intercepts, that is, the equation will have two roots or zeros.

2. If the discriminant is equal to zero, the quadratic equation will have only one real solution or one root.

3. If the discriminant is D<0, the quadratic equation will have no real roots (they will be complex roots.)

Therefore, the value of the discriminant in this case is:

`D=124`

And the function has two distinct real number zeros.