Question

02.03) identify all of the following solutions of square root of x plus 10 end root minus 4 equals x . (1 point) x = −6 x = −1 x = −6 and x = −1 none of the above

Answer 1

`√(x+10)-4=x\\ √(x+10)=x+4\\x+10=(x+4)^2=x^2+8x+16\\x^2+7x+6=0\\x^2+x+6x+6=0\\x(x+1)+6(x+1)=0\\(x+6)(x+1)=0\\x=-6 \ and \ x=-1`

x = -6 is an extraneous solution, Therefore, solution is x = -1.

Answer 2

The solution of given equation are x = −6 x = −1.

Explanation:

The given equation is

`√(x+10)-4=x`

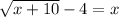
Add 4 on both sides.

`√(x+10)=x+4`

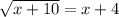
Square both side.

`x+10=(x+4)^2`

`x+10=x^2+8x+16`

`0=x^2+7x+6`

`0=x^2+6x+x+6`

`0=x(x+6)+1(x+6)`

`0=(x+6)(x+1)`

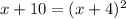
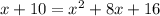
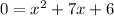
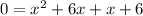
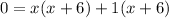
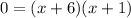
Use zero product property and equate each factor equal to 0.

`x+6=0\Rightarrow x=-6`

`x+1=0\Rightarrow x=-1`

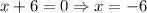
Therefore the solution of given equation are x = −6 x = −1.