Question

In the expression below, k is an integer.The expression can be simplified as,shown. Assume that the denominatorsare nonzero? x²+kx³ 428x + 12xx-2What is the value of k?A 8B 6C-6D -8

Answer 1

Given the equation:

`(x^4+kx^3)/(x^3-8x^2+12x)=(x^2)/(x-2)`

Let's assume the denominators are non zero and k is n integer.

Let's find the value of k.

First multiply both sides by the denominator by the left.

`\begin{gathered} (x^4+kx^3)/(x^3-8x^2+12x)*x^3-8x^2+12x=(x^2)/(x-2)*x^3-8x^2+12x \\ \\ \\ x^4+kx^3=(x^2(x^3-8x^2+12x))/(x-2) \end{gathered}`

Simplify the right side by factoring out x in the parentheses:

`\begin{gathered} x^4+kx^3=(x^2(x(x^2-8x+12))/(x-2) \\ \\ \text{ Now factor the numerator:} \\ x^4+kx^3=(x^2x(x-6)(x-2))/(x-2) \end{gathered}`

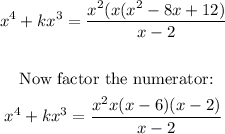
Cancel common factors:

`x^4+kx^3=x^3(x-6)`

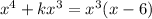
Solving further:

Apply distributive property on the left

`\begin{gathered} x^4+kx^3=x^4-6x^3 \\ \\ \text{ Subtract x}^4\text{ from both sides:} \\ x^4-x^4+kx^3=x^4-x^4-6x^3 \\ \\ kx^3=-6x^3 \end{gathered}`

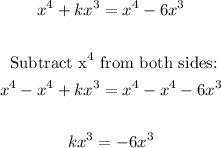
Divide both sides by x³:

`\begin{gathered} (kx^3)/(x^3)=(-6x^3)/(x^3) \\ \\ k=-6 \end{gathered}`

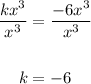
ANSWER:

C. -6