Question

9. y+2=0x+ 2 = 011.x-5y=45x + y = 4Determine if the graphs will show parallel or perpendicular lines, or neither.

Answer 1

9. We have the lines:

`\begin{gathered} y+2=0\rightarrow\text{ a horizontal line with constant value y = -2,} \\ x+2=0\rightarrow\text{ a vertical line with constant value x = -2.} \end{gathered}`

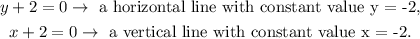
Plotting the lines, we get the following graph:

From the graph, we see that the lines are perpendicular.

11. We have the lines:

`\begin{gathered} x-5y=4, \\ 5x+y=4. \end{gathered}`

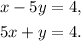
We rewrite the equations of the lines as:

`\begin{gathered} x-5y=4\rightarrow5y=x-4\rightarrow y=(1)/(5)x-(4)/(5), \\ 5x+y=4\rightarrow y=-5x+4. \end{gathered}`

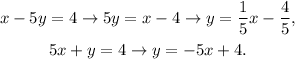
The general equation of a line with slope m and y-intercept b is:

`y=m\cdot x+b\text{.}`

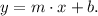
The slopes of the lines are:

`\begin{gathered} m_1_{}=(1)/(5), \\ m_2=-5. \end{gathered}`

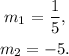
Two lines with slopes m1 and m2 are perpendicular if they satisfy the equation:

`m_1\cdot m_2=-1.`

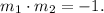
Replacing the values above, we get:

`m_1\cdot m_2=(1)/(5)\cdot(-5)=-1\text{ }✓`

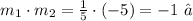
So we conclude that the lines are perpendicular.

Answer

9. Perpendicular

11. Perpendicular