Question

The side lengths of a 30-60-90 triangle are in the ratio 1 : square root of 3 : 2. What is tan 30°?

Answer 1

We can represent the information given in the question in picture form.

To find the tan of angle 30, we will proceed thus:

`\tan \theta=(opposite)/(adjacent)`

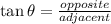
From the image above:

opposite side = 1

Adjacent side =

`\sqrt[]{3}`

Substitute the above given into the tan expression above

`\begin{gathered} \tan 30=\frac{1}{\sqrt[]{3}} \\ \tan 30=\frac{1}{\sqrt[]{3}}*\frac{\sqrt[]{3}}{\sqrt[]{3}} \\ \tan 30^o=\frac{\sqrt[]{3}}{3} \end{gathered}`

The correct answer is B.