PART A:
In order to calculate (fog)(x), that is, f(g(x)), we need to use g(x) as the input value (value of x) of f(x).
So we have:
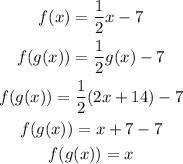
PART B:
Let's use f(x) as the input value of g(x):
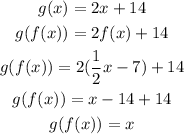
PART C:
When two functions are inverse to each other, we have the following property:
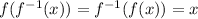
Since the composite functions of f(x) and g(x) are equal to x, therefore f(x) and g(x) are inverse functions.