Question

Explain why the triangles are similar. Then find the missing length, x. Choose the reason that the triangles are similar.

Answer 1

Question 1:

- Two triangles are similar if they have the exact same angles

- From the diagram given, the two triangles have right-angles, and vertically opposite angles (v) shown below:

- Since the sum of angles in a triangle is 180 degrees, and we know that the two triangles have 90 degrees and angle (v) in common, it implies that the third angle of both triangles must also be equal.

- Thus, the first answer is OPTION C

Question 2:

- To find the value of x, we use the property of similar triangles which states that the ratio of corresponding sides of similar triangles are equal.

- Thus, we can say:

`\begin{gathered} (22)/(11)=(x)/(8) \\ \\ (x)/(8)=2 \\ \\ \therefore x=16 \end{gathered}`

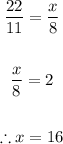
x = 16

Final Answer

- The first answer is OPTION C

x = 16