Question

Find the angle of elevation of the sun from the ground to the top of a tree when a tree that is 10 yards tall casts a shadow 14 yards long. Round to the nearest degree. o 54 degrees. o 36 degrees. o 46 degrees. o 44 degrees

Answer 1

Here is the solution of the given problem above.
Given: Height of tree = 10 yards
Shadow of the tree = 14 yards
? = Angle of elevation of the sun from the ground to the top of the tree
In this problem, we are going to use the inverse tangent trigonometric identity.
The correct answer would be 35.5 degrees. Round this off to the nearest degree and we get 36. Therefore, the correct answer would be 36 degrees.

Answer 2

The angle of elevation of the sun from the ground to the top of a tree is
`36^(\circ)`.

Explanation:

As given

The sun from the ground to the top of a tree when a tree that is 10 yards tall casts a shadow 14 yards long.

Now by using the trignometric identity .

`tan\theta =(Perpendicular)/(Base)`

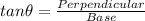
As figure is given below .

AB = Perpendicular = 10 yards

BC = Base = 14 yards

Putting all the values in the trignometric identity .

`tan\theta =(AB)/(BC)`

`tan\theta =(10)/(14)`

`\theta =tan^(-1)((10)/(14))`

`\theta =36^(\circ)`

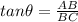
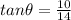
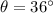
Therefore the angle of elevation of the sun from the ground to the top of a tree is
`36^(\circ)`.